相信不久前大家已经被这个粒子动画给刷屏了吧：

之前看过很多人都在分析跟这个效果相关的跨窗口通信技术，尽管这样是挺好，但我依旧有点纳闷：为什么没有人讲讲背后的粒子特效是怎么实现的呢？

于是乎，我花了一整个周末，把这个粒子特效给肝了出来。尽管可能跟原特效相比有一点差距，但也表明了这种效果是可以实现的。

在线体验：https://entangled-fxhash.netlify.app/

本文就让我们来看看实现这个粒子特效有哪些要点吧~

GPGPU

当我第一眼看到原特效时，发现那个球体是由大量的粒子组成的，第一反应就是THREE.Points，但是又转念一想，光这个是不够的，因为在粒子量足够大的情况下，同时渲染大量的运动粒子肯定会遇到性能上的瓶颈。

然后，我又想到了另一个技术——GPGPU，中文翻译是“图形处理器通用计算”，尽管这个概念看上去很复杂，但其实也很简单——利用GPU的并行特性来执行一些和图形渲染无关的计算任务，如模拟粒子系统等。在粒子非常多的情况下，用它就能满足性能上的需求。

three.js的官方文档上有一个模拟鸟群飞行的效果，就用到了这个技术，可以把鸟群飞行看作是一个不断运动着的粒子系统。

那么如何使用GPGPU呢？大致步骤如下：

1. 创建GPGPU对象，three.js里是GPUComputationRenderer；
2. 创建数据纹理，用来存储需要GPU计算的数据；
3. 创建GPGPU变量，每个变量需要一个对应的Compute Shader（计算着色器），用来处理变量的计算逻辑；
4. 初始化GPGPU，并在渲染循环中使其不断计算，将GPGPU变量计算得来的结果作为纹理变量赋给需要的材质。

以下是我的粒子效果用到的相关代码：

const width = 512;
const size = 256;
const count = width ** 2; // 我们总共要实时计算 512x512=262144 个粒子！

// 创建GPGPU对象(kokomi.GPUComputer 是一个对 GPUComputationRenderer 的封装)
const gpgpu = new kokomi.GPUComputer(this.base, {
  width,
});
// 创建数据纹理
const posDt = gpgpu.createTexture();
const data = posDt.image.data;

// 为数据纹理填充随机数据
for (let i = 0; i < data.length; i++) {
  data[i * 4 + 0] = THREE.MathUtils.randFloatSpread(size);
  data[i * 4 + 1] = THREE.MathUtils.randFloatSpread(size);
  data[i * 4 + 2] = THREE.MathUtils.randFloatSpread(size);
  data[i * 4 + 3] = 1;
}

// 创建GPGPU变量
const posVar = gpgpu.createVariable(
  "texturePosition",
  testObjectComputeShader,
  posDt,
  {
    uFreq: {
      value: 1,
    },
    ...
  }
);

// 初始化GPGPU
gpgpu.init();

粒子的本体还是用THREE.Points，只不过geometry用的是自定义的BufferGeometry，里面可以填充一些随机的位置数据position，同时也要加上用来采样GPGPU纹理的UV坐标reference。

const geometry = new THREE.BufferGeometry();
const positions = new Float32Array(count * 3);
const references = new Float32Array(count * 2);
for (let i = 0; i < width; i++) {
  for (let j = 0; j < width; j++) {
    const idx = i + j * width;
    positions[idx * 3 + 0] = Math.random();
    positions[idx * 3 + 1] = Math.random();
    positions[idx * 3 + 2] = Math.random();
    references[idx * 2 + 0] = i / width;
    references[idx * 2 + 1] = j / width;
  }
}
geometry.setAttribute("position", new THREE.BufferAttribute(positions, 3));
geometry.setAttribute("reference", new THREE.BufferAttribute(references, 2));

材质的话就用自定义着色器材质ShaderMaterial。

const material = new THREE.ShaderMaterial({
  vertexShader: testObjectVertexShader,
  fragmentShader: testObjectFragmentShader,
  uniforms: {
    texturePosition: {
      value: null,
    },
    uPointSize: {
      value: 1,
    },
    uPixelRatio: {
      value: this.base.renderer.getPixelRatio(),
    },
  },
  transparent: true,
  blending: THREE.AdditiveBlending,
  depthWrite: false,
});

顶点着色器中，我们要采样GPGPU帮我们计算得来的粒子位置。

uniform float uPointSize;
uniform float uPixelRatio;

uniform sampler2D texturePosition;

attribute vec2 reference;

void main(){
    vec3 p=texture(texturePosition,reference).xyz;
    gl_Position=projectionMatrix*modelViewMatrix*vec4(p,1.);

    gl_PointSize=uPointSize*uPixelRatio;
}

片元着色器直接输出粒子的颜色即可。

void main(){
    vec4 col=vec4(0.,1.,0.,1.);
    gl_FragColor=col;
}

然后就是创建微粒对象，并将它放到场景中，在渲染循环中给它的材质注入GPGPU计算得来的纹理数据。

const points = new THREE.Points(geometry, material);
this.scene.add(points);

this.update(() => {
  const mat = points.material;
  mat.uniforms.texturePosition.value = gpgpu.getVariableRt(posVar);
});

准备工作都已到位，接下来让我们开始进入真正的重头戏——Compute Shader。

Compute Shader

计算着色器的格式跟片元着色器类似，都是输出gl_FragColor，只不过这里的color代表的是GPU变量的值，在这里，我们用texturePosition作为了GPU变量，也就是粒子的位置，在着色器顶部声明好它。

uniform sampler2D texturePosition;

在主函数中，我们计算好UV坐标，并用它来采样texturePosition纹理。

void main(){
    vec2 uv=gl_FragCoord.xy/resolution.xy;
    vec3 pos=texture(texturePosition,uv).xyz;
    gl_FragColor=vec4(pos,1.);
}

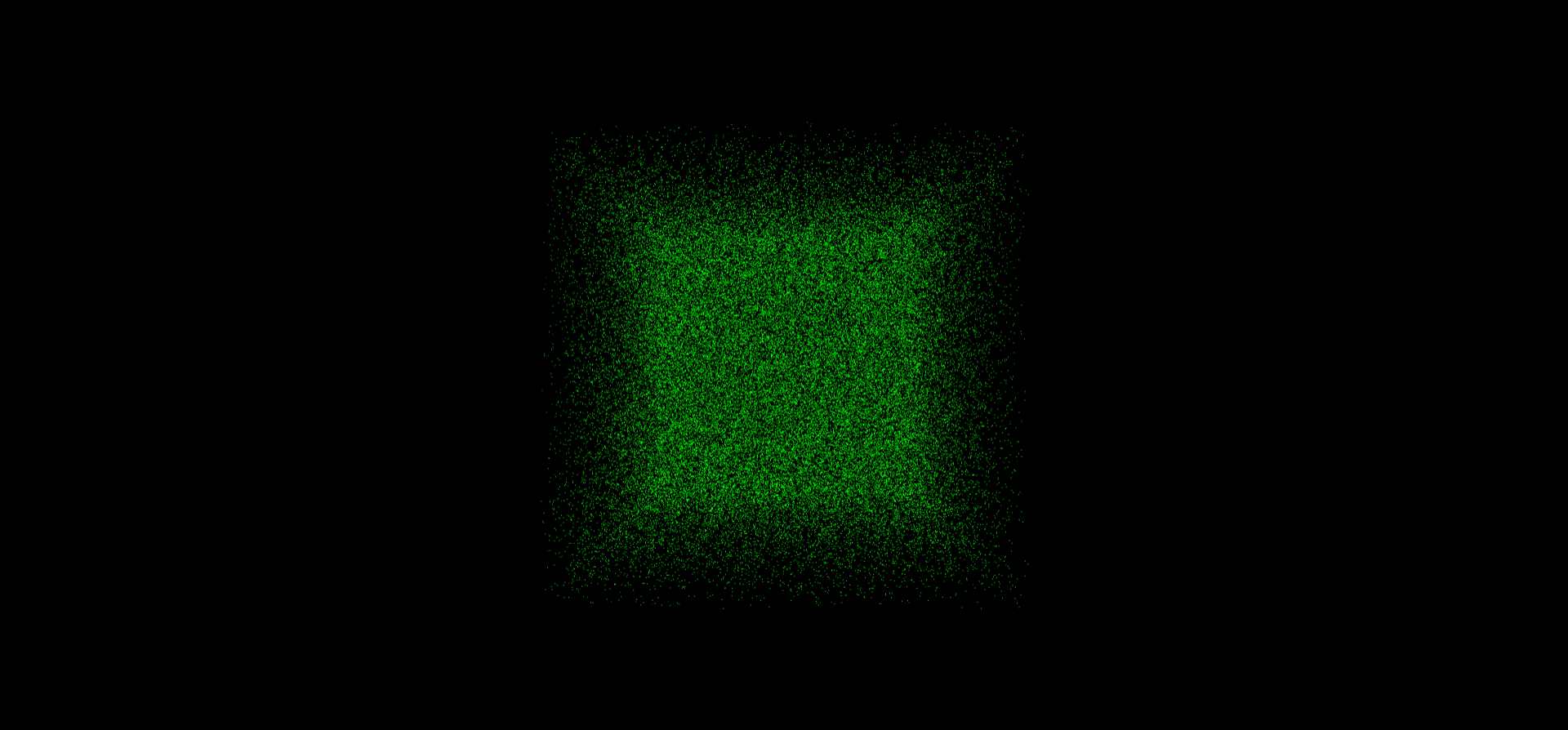
这里我们直接输出了位置纹理的原始数据，可以看到就是一堆随机的离散点。

是时候让这些点动起来了！给位置变量pos应用噪声函数吧，我选择了卷曲噪声curl。

这里用到了Shader函数库lygia，里面有很多实用的噪声函数。

#include "/node_modules/lygia/generative/curl.glsl"

void main(){
    vec2 uv=gl_FragCoord.xy/resolution.xy;
    vec3 pos=texture(texturePosition,uv).xyz;
    pos=curl(pos);
    gl_FragColor=vec4(pos,1.);
}

之前离散的点立马就变成了一个美丽的噪声球体。

除了单个卷曲噪声外，我们还可以用fbm，产生一个更加混沌的结果。

vec3 fbm(vec3 p){
    vec3 value=p;
    float amplitude=.5;
    float frequency=2.;
    float lacunarity=2.;
    float persistance=.5;
    float scale=.5;
    int octaves=1;

    for(int i=0;i<octaves;i++){
        vec3 noiseVal=curl(value*frequency*scale);

        value+=amplitude*noiseVal;
        frequency*=lacunarity;
        amplitude*=persistance;
    }

    return value;
}

void main(){
    vec2 uv=gl_FragCoord.xy/resolution.xy;
    vec3 pos=texture(texturePosition,uv).xyz;
    pos=curl(pos*uFreq);
    pos=fbm(pos);
    gl_FragColor=vec4(pos,1.);
}

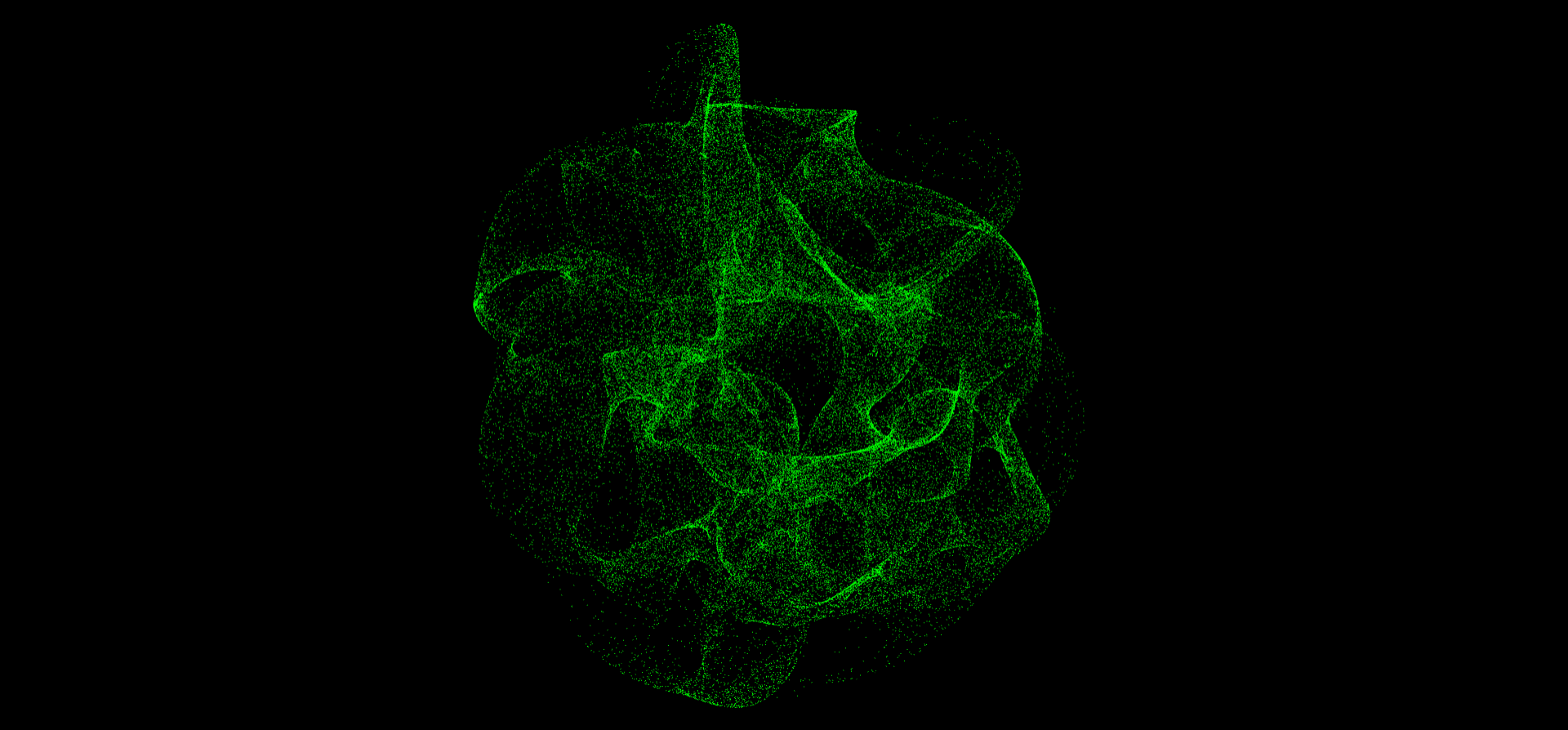
但这个结果太混沌了，跟之前的球体相差有点大。我们可以用mix函数来将它和球体有机地混合起来，混合因子也可以用其他的噪声函数来计算。

void main(){
    vec2 uv=gl_FragCoord.xy/resolution.xy;
    vec3 col=vec3(0.);
    vec3 pos=texture(texturePosition,uv).xyz;
    pos=curl(pos*uFreq);
    col=pos;
    vec3 pos2=texture(texturePosition,uv).xyz;
    pos2=curl(pos2*uFreq);
    pos2=fbm(pos2);
    col=pos2;
    float mixFactor=0.;
    mixFactor=cnoise(pos+iTime)*.5;
    col=mix(pos,pos2,mixFactor);
    gl_FragColor=vec4(col,1.);
}

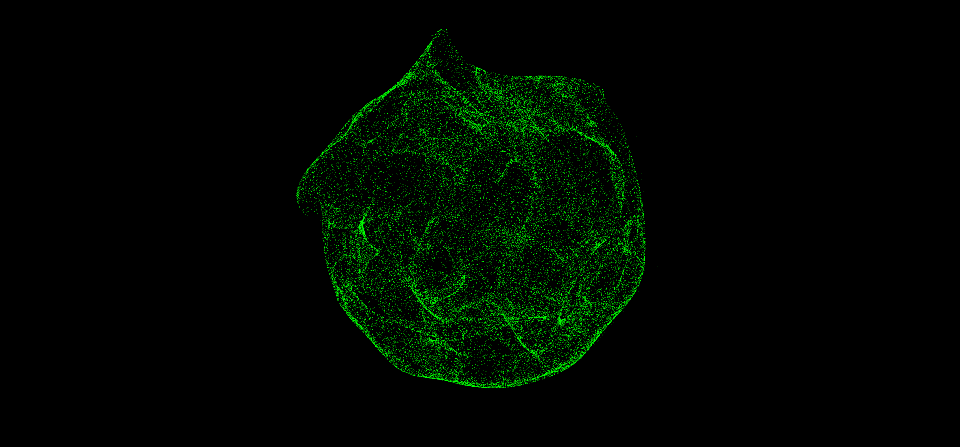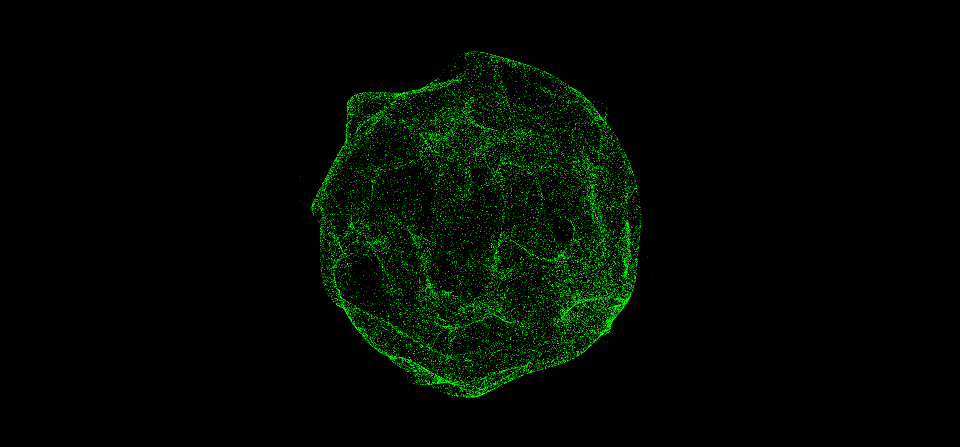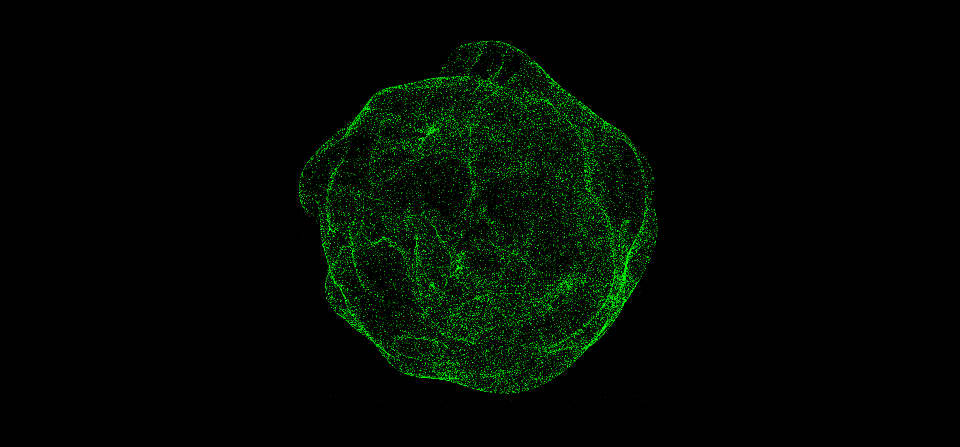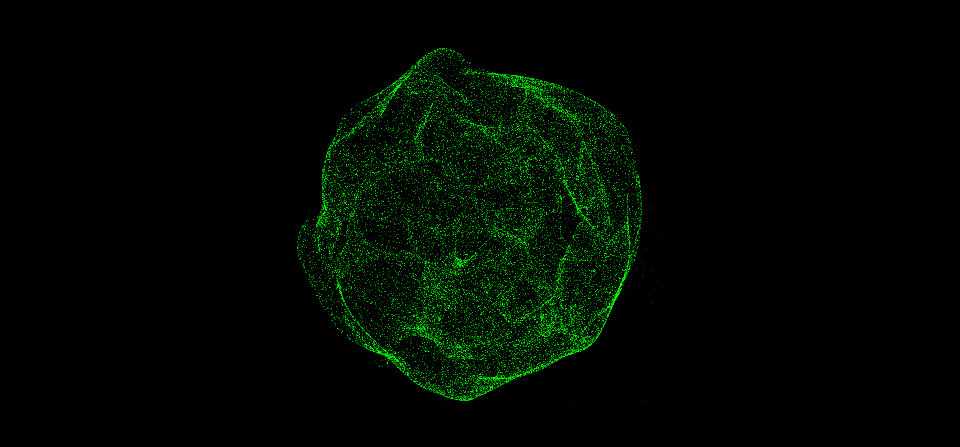
此外，我们可以做一个拉伸球的动画，用作后面纠缠动画的基础，思路如下：定义一个牵引点，用sdf函数算出牵引距离，再求得牵引方向向量，给位置变量应用它们的乘积即可。

#include "/node_modules/lygia/sdf/boxSDF.glsl"

void main(){
    vec2 uv=gl_FragCoord.xy/resolution.xy;

    ...

    vec3 attract=uAttract;
    float attractX=abs(attract.x);
    float d=boxSDF(col-attract,vec3(attractX,.25,.25));
    vec3 dir=normalize(col-attract);
    col-=dir*smoothstep(.2,.0,d)*(attractX-1.);

    gl_FragColor=vec4(col,1.);
}

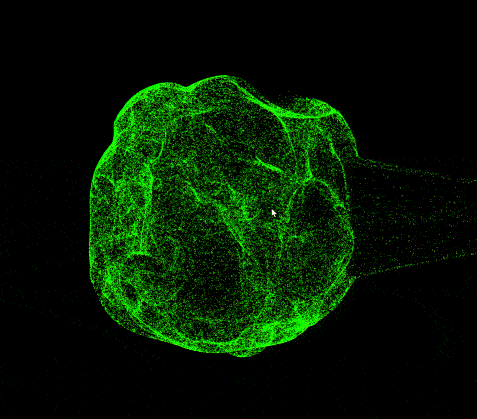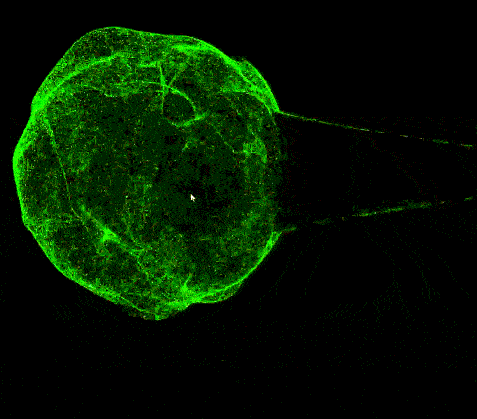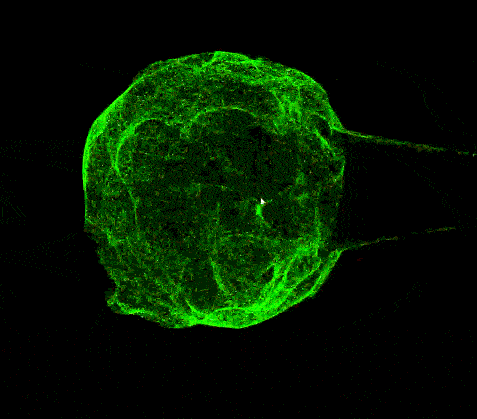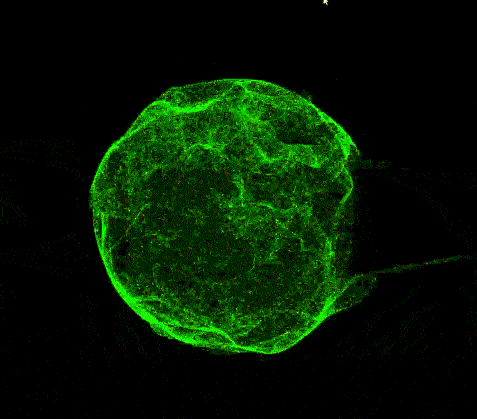
至于两球相互纠缠，emmmm，说实话我直接用了原作者开源的项目里的WindowManager来实现的，把里面的方块替换成了我的粒子球体，最终结果就是文章开头的那个动画。

最后

粒子效果本身差不多就这样完成了。还有一些待优化的点：

1. 不用卷曲噪声“逃课”，用更加精美的扭曲方式来美化球体。
2. 纠缠动画有一点生硬，并不像原效果那样丝滑、连贯。

主要还是第 2 点吧，感觉原作者是用了一种特定的算法来实现的，只可惜我不会 QAQ，还得继续努力呢~

源码

Github：https://github.com/alphardex/entangled